| Sketch2Go 0.84 |
|
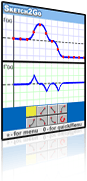
Sketch2Go is a qualitative graphing tool. Graphs are sketched using seven icons representing constant, increasing, and decreasing functions that change at constant, increasing, or decreasing rates. |
Description
Sketch2Go encourages visual exploration of phenomena by providing qualitative indication of the ways in which the sketch drawn by the user changes. The sketch is a diagrammatic representation that attempts to help the viewer focus on the principles rather than on tedious details of the represented phenomenon. Phenomenon can refer to processes outside of mathematics (e.g., physical temporal phenomena) or to mathematical phenomena (e.g., a function with three extrema). Moving students beyond plotting and reading points to interpreting the global meaning of graphs and the functional relationships that they describe has been identified as a major goal of mathematics education.
Tools like Sketch2Go enable the bypassing of algebraic symbols as the only channel into mathematical representation, and motivate students to experiment with a given situation, analyze it, and reflect upon it, even when the situation is too complicated for them to approach symbolically. The visual analysis that emerges from work with such tools is different from that which arises from work with algebraic symbols or numerical tables.
Features
Sketch2Go is a qualitative graphing tool. Graphs are sketched using seven icons representing constant, increasing, and decreasing functions that change at constant, increasing, or decreasing rates. It is based on original R&D carried out by Schwartz and Yerushalmy (1995) and Shternberg & Yerushalmy (2001), who propose an intermediate bridging representation based on the function and its vocabulary. The seven graphic icons describe the change in both the function and its rate of change. Sketch2Go is a version of the Qualitative Derivative Grapher programmed by Alexander Zilber for CET (Centre for Educational Technology).
Mathematical modeling cannot be fully accomplished by this qualitative sign system of constant, increasing, and decreasing functions. But the set of seven signs supports forming a mathematical construction with language developed from acquaintance with physical scenarios, helping lay the foundations of learning pre-calculus and calculus. Sketch2Go supports the abstraction of everyday phenomena using a small set of mathematical signs that can be manipulated on screen as semi-concrete objects.
Suggested Activities
a modeling problem
a car is moving at a speed of 20 meters per second when the driver sees a ball rolling on the road. The driver’s reaction time is one second (reaction time is the time that passes between identifying the ball and pressing the brakes.) During that time the car continues at its constant speed. After the driver presses the brakes, the car decelerates for 7 seconds until it stops.
- Describe in a graph the distance the car traveled during from the time the driver saw the ball until the car stopped.
- What does the lower graph describe in this story?
- How would your graph change in each of the following situations: (1) the driver drove faster; (2) the driver was drunk; (3) it was a rainy day.
Using sketches to prove derivative rules
Sketch examples of functions that would fulfill the constraints listed below.
Write the properties that the functions represent or argue why you could not find such functions:
- Continuous functions whose derivatives are increase monotonically
- Continuous functions that have derivative functions with exactly a single maximum
- Continuous functions with derivative functions that have a discontinuity or some sort
- Functions with discontinuity that have continuous derivative functions
- Functions that have continuous derivative functions and a second derivative with discontinuity