| Quad2Go 0.84 |
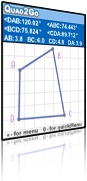
|
Quad2Go is a handy tool for learning about quadrilaterals by generating examples, observing, and experimenting with examples with a view toward forming generalized conjectures. |
Description
Explorations with Quad2Go are especially appropriate for 11-12 year old students. Teaching geometry to students of this age focuses on the critical attributes of quadrilaterals and on the hierarchical relations among them. Learning means identifying critical attributes and non-critical attributes. For example, "four sides," "two pairs of parallel sides," or "two pairs of equal opposite angles" are some of the critical attributes of a parallelogram; "two long sides and two short sides" or "two acute angles and two obtuse angles" are non-critical attributes. Learning in this sense means learning to analyze the attributes of different quads, to distinguish between their critical and non-critical attributes, and learning the hierarchy among quads. Quad2Go provides many examples of randomly constructed quads. Each example can be changed by dragging either its vertices or sides.
Features
Quad2Go is a handy tool for learning about quadrilaterals by generating examples, observing, and experimenting with examples with a view toward forming generalized conjectures. Similarly to frequently used Dynamic Geometry Environments (DGE) such as the Geometric Supposer, Cabri Geometry, and the Geometer Sketchpad, Quad2Go offers geometric objects, tools to manipulate them, and measurement tools. It is limited to quadrilaterals and the construction of diagonals. Quad2Go allows users to construct, view, and transform quadrilaterals compatible with the ones constructed with straight edge and compass, to measure lengths, angles, and areas, and to manipulate the construction by dragging and transforming its shape. Dragging allows changing a shape by direct translation of parts of its components on the screen. Learning by DGE is closely related to theories of constructivist learning, in which meaning is constructed through the learner’s active participation.
Suggested Activities
An exploration of hierarchy of quads
Use the Shapes menu to construct parallelograms, kites, trapezoids, and rhombi.
From the Quad2Go menu choose to view parallelograms.
Here is a construction of a parallelogram. Why?
Did you obtain a rectangle as one of the parallelograms? Do you agree that it is a rectangle? Do you think you can get a rectangle? Why?
Under which shape’s choice would you expect to obtain a square? Why?
An exploration task regarding non standard classification
a square, a rhombus, and a kite are quads that share the following property: the angle between their diagonals is a right angle. Quads with this property are called orthodiagonal quads.
Discover other special properties of this class of quads.
Implementing knowledge about triangles
In any convex quadrilateral the two diagonals create eight triangles. For each type of given quadrilateral:
Identify the 8 triangles
Identify 4 congruent triangles; explain your decision.
Identify 2 congruent triangles; explain your decision.
Identify similar triangles; explain your decision.